不可测集(Vatali Set)的构造
理想测度
在我们心里, 在实数域中最”美好”的测度应该具有这几条性质:
-
$\lambda :{\mathscr P}(R) \to R{_ + } \cup \left\{ \infty \right\}$
-
$\lambda ([a,b]) = b - a$
-
$\lambda (A + x) = \lambda (A)$ (平移不变)
-
$\lambda (\mathop \bigsqcup \limits_{j \ge 1} {A_j}) = \sum\limits_{j \ge 1} {\lambda ({A_j})}$ ($\sigma$-可加)
在这样的测度下, 是否有不可测的集合存在?
一些定义
若$x,y \in R$,且$y - x \in Q$(有理数集),则称$x \sim y$(x和y等价).记为$[x] = \left\{ {y \in R\;|\;y - x \in Q} \right\}$.
$\Lambda$:所有$R$中元素的等价类组成的集合
$\Omega$:只取$\Lambda$中每个等价类的一个元素组成的集合。且$\Omega \in (0,1)$。
用类似数论中的语言, $\Lambda$是$\mathbb R$以上述等价关系为模的等价类的集合.
这个集合是不可数的, 否则因为每个等价类是可数的, $\mathbb R$作为这些等价类的并集也将是可数的.
几个引理
引理一 (测度函数的单调性)
若$E \subseteq F$,则$\lambda (E) \le \lambda (F)$
证明:
$F = E \cup (F|E)$.
由测度函数定义第四条,$\lambda (F) = \lambda (E \cup (F|E)) = \lambda (E) + \lambda (F|E)$。
而$\lambda (F|E) \ge 0$,所以$\lambda (E) \le \lambda (F)$.
引理二
对$\forall p,q \in Q$,要么$\Omega + p = \Omega + q$,要么$(\Omega + p) \cap (\Omega + q) = \emptyset$.
也就是说, 两个这样的等价类要么相等, 要么不交
证明:
反证, 假设$x\in (\Omega + p) \cap (\Omega + q)$, $p\neq q$,
则存在$\alpha \in \Omega$,使得$x = \alpha + p$.同样,存在$\beta \in \Omega$,使得$x = \beta + q$.
则$\alpha-\beta=q-p$.
因为$p-q \in Q$,所以$\alpha-\beta \in Q$,由等价定义知,$\alpha \sim \beta$。
再由$\Omega$的定义, $\alpha = \beta$, 那么$p = q$
证毕。
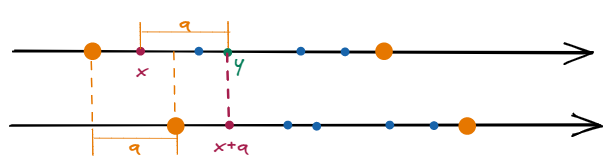
对这个证明可以这样理解:
为了画图方便, 我在这里先假设$p=0$,$q \neq 0$. 那么$\Lambda$中的某个元素$x$向右平移$q$后,不可能有$\Lambda$中元素$y$和$x+q$重合(因为$\Lambda$中每个等价类只取一个, 而$x$和$x+q$是一个等价类的).
不可测集的构造
证明$\lambda$函数在Vatali集$\Omega$上的定义存在矛盾,即$\Omega$是不可测的.
因为 $\sum_{q \in \mathbb{Q},-1<q<1}(\Omega+q) \subseteq(-1,2)$
\(\lambda\left(\sum_{q \in \mathbb{Q},-1<q<1}(\Omega+q)\right) \leq \lambda((-1,2))=3\)
再由可数可加性和平移不变性得
\(\lambda\left(\sum_{q \in \mathbb{Q},-1<q<1}(\Omega+q)\right)=\sum_{q \in \mathbb{Q},-1<q<1} \lambda(\Omega+q)=\sum_{q \in \mathbb{Q},-1<q<1} \lambda(\Omega) \leq 3\)
知
\(\lambda(\Omega)=0\)
故
\(\sum_{q \in \mathbb{Q},-1<q<1} \lambda(\Omega) = 0\)
但是 $(0,1) \subseteq \sum_{q \in \mathbb{Q},-1<q<1}(\Omega+q) , \lambda((0,1))=1$ ,
这样又可以得到
\(\lambda\left(\sum_{q \in \mathbb{Q},-1<q<1}(\Omega+q)\right)=\sum_{q \in \mathbb{Q},-1<q<1} \lambda(\Omega+q)=\sum_{q \in \mathbb{Q},-1<q<1} \lambda(\Omega) \geq 1\)
这是矛盾的.$\square$
解释一下 $(0,1) \subseteq \sum_{q \in \mathbb{Q},-1<q<1}(\Omega+q)$
任取 $x \in(0,1)$ 則 $x=[x]+q,[x] \in \Omega \subseteq(0,1), q \in \mathbb{Q}$
故 $q=x-[x] \in(-1,1)$ .
这里用[x]表示x所属的那个等价类的代表元
